52 Hands
In the standard game of poker, each player gets5 cards and places a bet, hoping his cards are 'better'than the other players' hands.
The game is played with a pack containing 52 cards in 4 suits, consisting of:
13 hearts:
13 diamonds
13 clubs:
13 spades:
♥ 2 3 4 5 6 7 8 9 10 J Q K A
♦ 2 3 4 5 6 7 8 9 10 J Q K A
♣ 2 3 4 5 6 7 8 9 10 J Q K A
♠ 2 3 4 5 6 7 8 9 10 J Q K A
STEAM Lab for Kids: 52 Creative Hands-On Projects for Exploring Science, Technology, Engineering, Art, and Math (Lab for Kids, 17) Heinecke, Liz Lee on Amazon.com.FREE. shipping on qualifying offers. STEAM Lab for Kids: 52 Creative Hands-On Projects for Exploring Science, Technology, Engineering, Art. This subpart- (a) Gives instructions for using part 52, including the explanation and use of provision and clause numbers, prescriptions, prefaces, and the matrix; (b) Prescribes procedures for incorporating, identifying, and modifying provisions and clauses in solicitations and contracts, and for using alternates; and (c) Describes the derivation of FAR provisions and clauses.
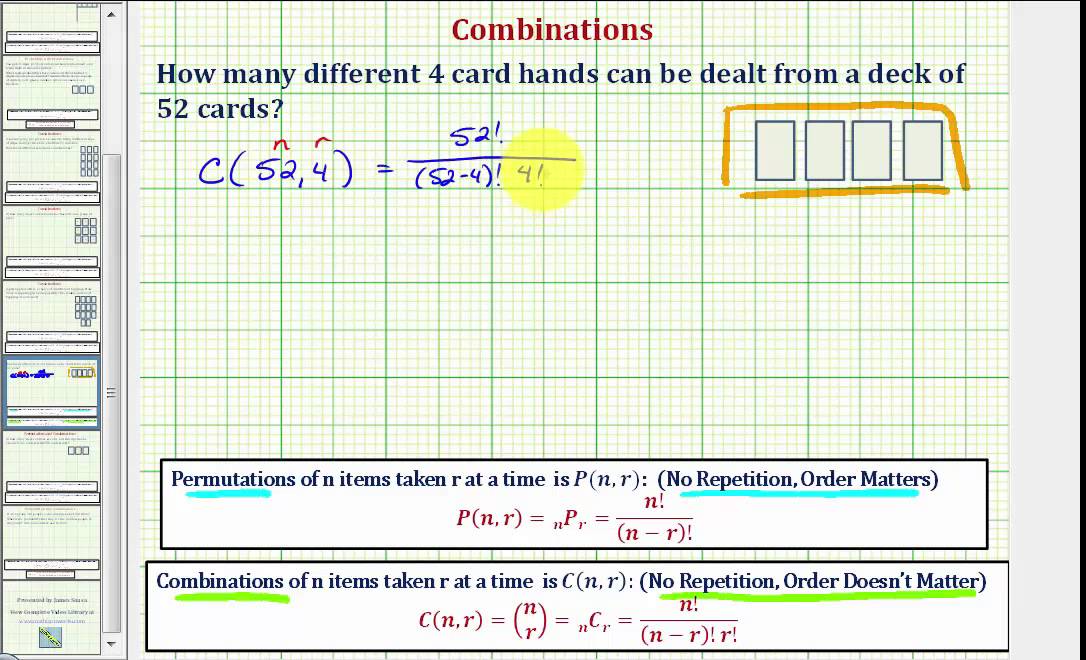
The number of different possible poker hands is found by counting the number of ways that 5 cards can be selected from 52 cards, where the order is not important. It is a combination, so we use `C_r^n`.
The number of possible poker hands
`=C_5^52=(52!)/(5!xx47!)=2,598,960`.
Royal Flush
The best hand (because of the low probability that it will occur) is the royal flush, which consists of 10, J, Q, K, A of the same suit. There are only 4 ways of getting such a hand (because there are 4 suits), so the probability of being dealt a royal flush is
`4/(2,598,960)=0.000 001 539`
Straight Flush
The next most valuable type of hand is a straight flush, which is 5 cards in order, all of the same suit.
For example, 2♣, 3♣, 4♣, 5♣, 6♣ is a straight flush.

For each suit there are 10 such straights (the one starting with Ace, the one starting with 2, the one starting with 3, ... through to the one starting at 10) and there are 4 suits, so there are 40 possible straight flushes.
The probability of being dealt a straight flush is
`40/(2,598,960)=0.000 015 39`
[Note: There is some overlap here since the straight flush starting at 10 is the same as the royal flush. So strictly there are 36 straight flushes (4 × 9) if we don't count the royal flush. The probability of getting a straight flush then is 36/2,598,960 = 0.00001385.]
The table below lists the number ofpossible ways that different types of hands can arise and theirprobability of occurrence.
Ranking, Frequency and Probability of Poker Hands
| Hand | No. of Ways | Probability | Description |
| Royal Flush | 4 | 0.000002 | Ten, J, Q, K, A of one suit. |
| Straight Flush | 36 | 0.000015 | A straight is 5 cards in order. (Excludes royal and straight flushes.) An example of a straight flush is: 5, 6, 7, 8, 9, all spades. |
| Four of a Kind | 624 | 0.000240 | Example: 4 kings and any other card. |
| Full House | 3,744 | 0.001441 | 3 cards of one denominator and 2 cards of another. For example, 3 aces and 2 kings is a full house. |
| Flush | 5,108 | 0.001965 | All 5 cards are from the same suit. (Excludes royal and straight flushes) For example, 2, 4, 5, 9, J (all hearts) is a flush. |
| Straight | 10,200 | 0.003925 | The 5 cards are in order. (Excludes royal flush and straight flush) For example, 3, 4, 5, 6, 7 (any suit) is a straight. |
| Three of a Kind | 54,912 | 0.021129 | Example: A hand with 3 aces, one J and one Q. |
| Two Pairs | 123,552 | 0.047539 | Example: 3, 3, Q, Q, 5 |
| One Pair | 1,098,240 | 0.422569 | Example: 10, 10, 4, 6, K |
| Nothing | 1,302,540 | 0.501177 | Example: 3, 6, 8, 9, K (at least two different suits) |
Question
The probability for a full house is given above as 0.001441. Where does this come from?
Answer
Explanation 1:
Probability of 3 cards having the same denomination: `4/52 xx 3/51 xx 2/50 xx 13 = 1/425`.
(There are 13 ways we can get 3 of a kind).
The probability that the next 2 cards are a pair: `4/49 xx 3/48 xx 12 = 3/49`
(There are 12 ways we can get a pair, once we have already got our 3 of a kind).
The number of ways of getting a particular sequence of 5 cards where there are 3 of one kind and 2 of another kind is:
`(5!)/(3!xx2!)=10`
So the probability of a full house is
`1/425 xx 3/49 xx 10 ` `= 6/(4,165)` `=0.001 440 6`
Explanation 2:
Number of ways of getting a full house:
`(C(13,1)xxC(4,3))` `xx(C(12,1)xxC(4,2))`
`=(13!)/(1!xx12!)` `xx(4!)/(3!xx1!)` `xx(12!)/(1!xx11!)` `xx(4!)/(2!xx2!)`
52 Handsworth Wood Road

`=3744`
52 Hands Fighting
Number of possible poker hands
52 Hand Block
`=C(52,5)` `=(52!)/(47!xx5!)` `=2,598,960`
So the probability of a full house is given by:
`P('full house')`
`='ways of getting full house'/'possible poker hands'`
`= (3,744)/(2,598,960)`
52 Crip Handshake
`=0.001 441`